About twelve years ago, in an exceptional situation, I experienced something I never had experienced before: extremely intense psychical (!) pain. The pain was in fact so intense, that I was sure that I could not survive it. Most fortunately (and for reasons I still don’t understand), the pain lasted only for about a second.
And since this day, there is this question waiting to be answered: if such an extreme pain is possible, is there also a similar extremely intense pleasure possible? A feeling maybe orders of magnitude more pleasurable than an orgasm? Based on my experience this seems to be likely.
But then (of course!) comes the question: how can we find this holy grail of fun?
I recently decided to investigate a bit. I chose the example of a social interaction between two people. It could be sexual intercourse, but maybe also something completely different. What if I could convert my beliefs about the processes happening during such an interaction into formulas and algorithms (a mathematical model). This would allow me to search for input parameters (like behaviors, mindsets etc.) which lead to optimal outputs (e.g. pleasure of the two interacting people).
Would this be science? No, not without trying to verify/falsify the model with experimental data and a careful analysis. Does such an undertaking still make sense? I think yes. If it makes sense to develop personal models for social interactions, then it makes absolutely sense too to explore these models in great detail. And to construct such models is something everybody does (if only subconsciously in many cases). And: could it be a fun weekend project? Sure!
Therefore I decided to formulate as precisely as possible what I believed how such interactions work and write some python code to simulate the process.
I have uploaded the complete python code for this experiment to my Github page.
Here we go:
The most compact formulation of the my model would be a set of differential equations. But to write them down here would scare away many readers (and, due to my limited math skills, I could not do much with them anyways). So I’m going to skip this step and present some python simulation code instead (which is actually numerically solving the equations I am denying you), which - I believe - is much more accessible for most.
My model consists of the following equations (description followed by python code):
- The total pleasure P a person experiences during a social interaction is the sum of the pleasure the person would experience alone (I call this the proper pleasure) and a fraction (= compassion) of the pleasure perceived from the other person (= social pleasure).
- Pleasure can, of course, also become negative (pain).
# Total pleasure is proper pleasure plus social pleasure felt
# But we feel only a fraction c (compassion) a of the partners pleasure
P1 = P1Proper + c1 * P1Social
P2 = P2Proper + c2 * P2Social
- The perception of the pleasure of the other person needs some time. The other person needs to emit signals of pleasure and they need to be received by the person. The social pleasure is therefore following the pleasure of the other person with some delay.
# The pleasure perceived by 1 is slowly approaching the pleasure of 2 (perception needs time)
# The rate of following is described by the perception rate p
P1Social += p1 * (P2 - P1Social) # P1Social is always slowly moving towards P2
P2Social += p2 * (P1 - P2Social) # P2Social is always slowly moving towards P1
- The proper pleasure of a person is influenced by what the other person does. This influence can be negative (other person does things the person does not like) or positive (other person does things the person likes). Also, the strength of this influence can vary. I also assume that this influence is proportional to the pleasure the other person experiences (each person is carefully trying her thing, accelerating as soon as some success = pleasure is experienced).
# The proper pleasure changes, depending on pleasure driven actions of partner
# this depends on the action influence rate i of the partner (can be negative!)
# if you are in pain, you cannot execute actions -> change is 0 for P < 0
P1ProperRaw += i2 * max(0,P2)
P2ProperRaw += i1 * max(0,P1)
- The proper pleasure must be limited to the pleasure we could experience alone (i.e. moderate pain to moderate pleasure).
# proper pleasure is limited to a max. of -1..1 (-100% to 100%) -> apply tanh
P1Proper = math.tanh(P1ProperRaw)
P2Proper = math.tanh(P2ProperRaw)
# a simpler way to limit the values to -1,..,1
#P1Proper = max(-1,min(1.0,P1ProperRaw))
#P2Proper = max(-1,min(1.0,P2ProperRaw))
Now we need to define some reasonable parameters and initial values:
# compassion fraction
c1 = 0.4
c2 = 0.3
# perception rates
p1 = 0.05
p2 = 0.05
# action influence
i1 = 0.05
i2 = 0.03
# initial values for proper pleasure
P1ProperRaw = 0.5 # fraction of max. proper pleasure, so must be in (-1,1)
P2ProperRaw = 0
And we can write now the complete simulation loop:
P1Social = 0 # Social pleasure always starts with 0 (need perception to build up)
P2Social = 0
P1Proper = math.tanh(P1ProperRaw)
P2Proper = math.tanh(P2ProperRaw)
for i in range(SIMULATION_STEPS):
# Total pleasure is proper pleasure plus social pleasure felt according to compassion c
# But we feel only a fraction c a of the partners pleasure
P1 = P1Proper + c1 * P1Social
P2 = P2Proper + c2 * P2Social
# The pleasure perceived by 1 is slowly approaching the pleasure of 2 (perception needs time)
# The rate of following is described by the perception rate p
P1Social += p1 * (P2 - P1Social) # P1Social is always slowly moving towards P2
P2Social += p2 * (P1 - P2Social) # P2Social is always slowly moving towards P1
# The proper pleasure changes, depending on pleasure driven actions of partner
# this depends on the action influence rate i of the partner (can be negative!)
# if you are in pain, you cannot execute actions -> change is 0 for P < 0
P1ProperRaw += i2 * max(0,P2)
P2ProperRaw += i1 * max(0,P1)
# proper pleasure is limited to a max. of 1 (100%) -> use tanh
P1Proper = math.tanh(P1ProperRaw)
P2Proper = math.tanh(P2ProperRaw)
if i in PRINT_AT_STEPS:
print(i,"P1",P1,"P1Proper",P1Proper,"P1Social",P1Social)
print(i,"P2",P2,"P2Proper",P2Proper,"P2Social",P2Social)
Let's discuss this code first briefly:
- If both initial values for the proper pleasure are zero, the pleasure of both persons will remain zero. Therefore: at least one of the persons must start with some feeling of fun!
- Note that the social pleasure of person 1 includes the pleasure of the person 2 which in turn (over the social pleasure of person 2) again includes the pleasure of person 1!
Now we have the problem that we dont know which parameters c,p,i etc. yield good results. So I wrote a second script to run the simulation with thousands of random combinations of parameters and plot them to find relationships:
results = []
for sim_no in range(NO_OF_SIMULATIONS):
c1 = random.uniform(0,1)
c2 = random.uniform(0,1)
p1 = random.uniform(0.001,0.1)
p2 = random.uniform(0.001,0.1)
i1 = random.uniform(-0.1,0.1)
i2 = random.uniform(-0.1,0.1)
P1ProperRaw = random.uniform(0,1)
P2ProperRaw = random.uniform(0,1)
P1,P2 = run_simulation(c1,c2,p1,p2,i1,i2,P1ProperRaw,P2ProperRaw,SIMULATION_STEPS)
results.append([c1,c2,p1,p2,i1,i2,P1ProperRaw,P2ProperRaw,P1,P2])
Let's have a look at some results. I made scatterplots with various variable combinations. In most cases, the algorithm seems to converge with the chosen initial values (more on this later).
If we look at the final pleasures alone, we get the following:
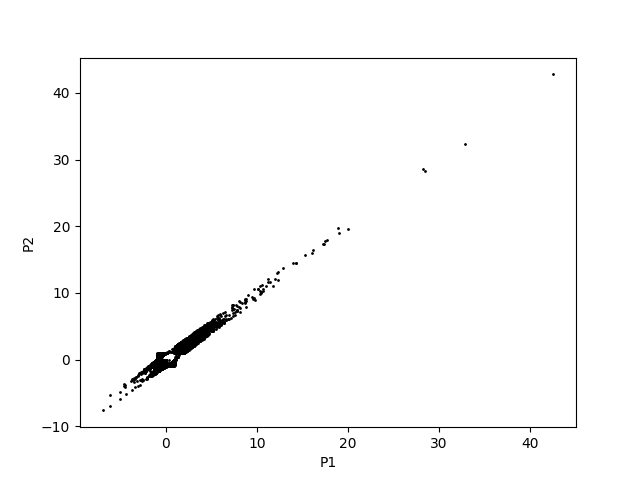
- Pleasure and pain are, at least in the extreme ends, a shared experience: if person 1 is in great pain (or pleasure), so is person 2.
- The vast majority of experiences happen in a very limited pleasure range. But there are some extreme outliers (up to 40 times the maximal proper pleasure!)
If we want to know which parameters contribute to great results, we have to plot against them:
The initial pleasure seems to be not very important (circle size proportional to the absolute value of P1, the color shows P1: blue=min to red=max):
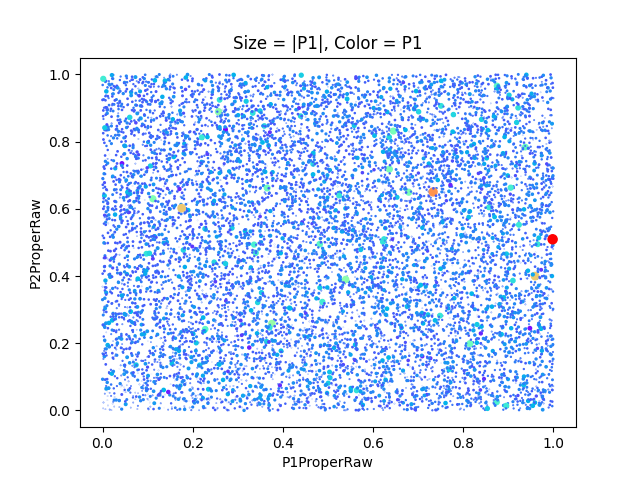The large dots are scattered all over the plot!
The perception rates seem to make no major difference too (at least after 1200 simulation steps):
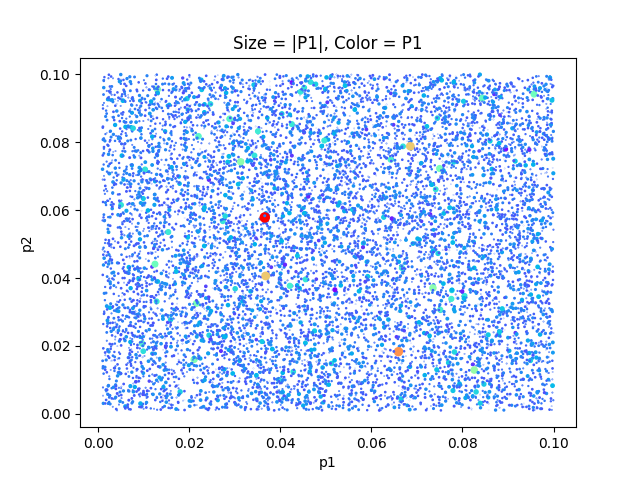
More interesting is the influence rate:
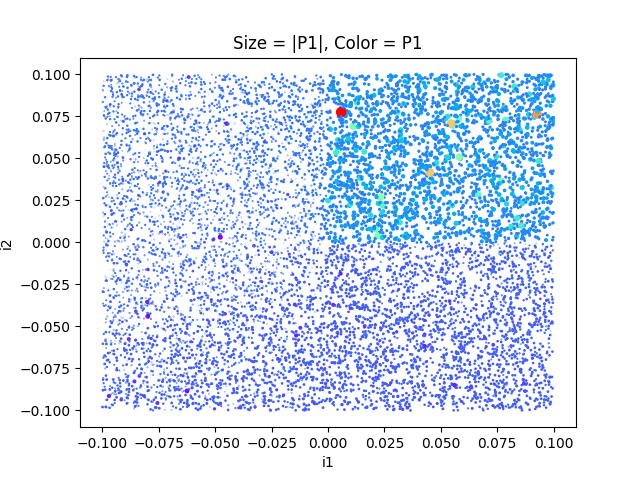
- Good results (and extremely good results) require both persons to act positively on the other person (upper right quadrant)!
Now let's look at the compassions:
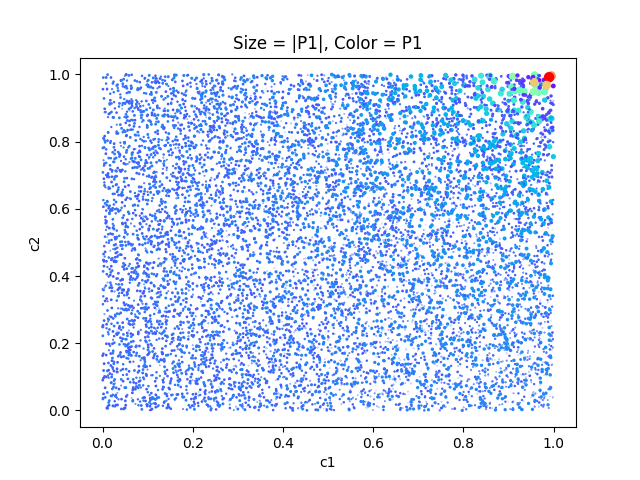
Now this is interesting!
- Good results require both persons to be very compassionate
- Extremely high pleasure requires a very high compassion (near 100%) from both partners
- High shared pain also requires high mutual compassion
Also, very interesting structures in the low pleasure range can be seen:
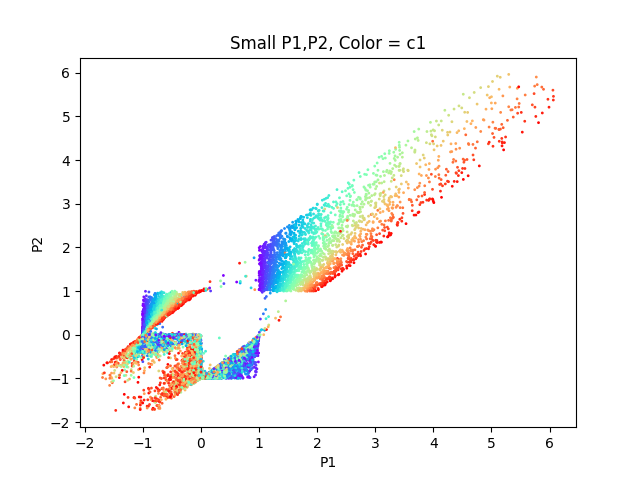
But this might be also numerical artefacts.
I will follow up on this. Stay tuned (but please don't take all this too seriously)!
The complete python code for this project is available for download on my Github page.
In the next blog post I will analyze the formulas presented in this blog post using mathematics.
Image on top: Shutterstock
Illustration: © Author
Follow me on X to get informed about new content on this blog.
